The second post in the series that started here. Apologies for the months-long delay! The third will go up later this week.
Quine claims that, for a certain class of languages, the substitutional and model-theoretic definitions of logical truth are equivalent:
(EQ-R) 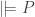 iff
iff 
Which languages? Ones that have two properties:
(P1) They are “rich enough for elementary number theory” (Philosophy of Logic, p. 53).
(P2) They are first-order. (In particular, completeness and a specific version of the Loewnheim-Skolem theorem hold for them.)
Here are today’s questions:
- What counts as being “rich enough for number theory”?
- How is this result consistent with the arguments of section 3 of the last post?
- What, exactly, is Quine’s argument? How does it work, and on what assumptions does it depend?
I won’t tackle these in order, though. I’ll start with 2, and then move on to 3. 1 will be covered towards the end.
Section 1: Motivation
Before getting into the nitty gritty, it’s worth taking a step back to ask why we — or Quine — should care, either about EQ-R or the full EQ.
First, consider how we would expect Etchemendy to react. Since the EQs hold, at best, only for a restricted class of languages, he will likely be unimpressed. Etchemendy’s approach in The Concept of Logical Consequence shows that he wants a perfectly general analysis which, when thrown an arbitrary language, will give the right predictions. Since we know a substitutional account generates bad predictions for at least some languages, by Etchemendy’s lights there’s no use continuing to go on about it.
Not so for Quine. He has little truck with the notion of an analysis. (If we could analyze logical consequence, we would have an instance of synonymy, which he famously decries.) As a pragmatist, the important question for him is, “What well-behaved definition will suit us best for our purposes?” And if our purposes keep us well within the limited class of languages for which an EQ result holds, then this tells us that, if the model-theoretic account works for our purposes, so does the substitutional.
For Quine, though, the result also goes two steps deeper. For one thing, Quine thinks there are reasons to use the substitutional account when we can for — unlike the model-theoretic one — we don’t have to deploy sets for the substitutional account. The objection here isn’t the “there are no sets, so let’s be substitutionalists” one — Quine eventually accepted sets, after all, thinking them indispensable to science — but rather that we should do as much as we can with as little as we can get away with, so if we’re not forced to, we should avoid appealing to them in our definition of logical consequence.
Second, and in Boolos’s eyes most important, Quine thinks the EQ results give an argument for identifying “logic” with first-order logic. (There is, I think, a real issue as to just what this identification means — both for us and for Quine — but set that aside.) We choose a logic just as we choose other theories: by seeing which does best at the various theoretical virtues. Since the EQ result, as well as completeness, apply only to first-order theories, only if logic is first-order can we collapse proof-theoretic, model-theoretic, and substitutional accounts of consequence. Quine sees this as a virtue, and thus grist for his “logic-is-first-order” mill.
Section 2: Reconciliation
Ok, next: resolving the last post’s puzzle. There, we saw that a counting sentence like
(E2) 
will count as a substitutional, but not a model-theoretic, truth, and thus threaten a counterexample to (EQ-R). How is Quine not worried about this? The answer comes a few pages after his argument, where we learn “Truths of identity theory [such as 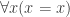 ] do not count as logical truths under the contemplated definitions of logical truth, since they are falsifiable by substituting other predicates for
] do not count as logical truths under the contemplated definitions of logical truth, since they are falsifiable by substituting other predicates for  .” (p. 61). Quine does not think that all substitution schemes take (E2) to (E2), for — unlike what Etchemendy assumed — he does not reckon the identity predicate one of the logical constants.
.” (p. 61). Quine does not think that all substitution schemes take (E2) to (E2), for — unlike what Etchemendy assumed — he does not reckon the identity predicate one of the logical constants.
That answers one side of the problem. But in standard textbook model-theoretic treatments of first-order logic with identity, 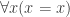 does come out true on all models. If this is not to be a further counterexample to EQ-R, Quine had better have a not-quite-so textbook model theory. And indeed he does. How his differs from the textbook depends on just what the textbook says.
does come out true on all models. If this is not to be a further counterexample to EQ-R, Quine had better have a not-quite-so textbook model theory. And indeed he does. How his differs from the textbook depends on just what the textbook says.
In some textbooks, the interpretation function of a model does not assign an extension to  . Rather, satisfaction-conditions for sentences of the form
. Rather, satisfaction-conditions for sentences of the form 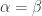 are hard-wired into the definitions of truth and satisfaction on a model. In other textbooks, the definitions of truth and satisfaction on a model don’t treat identity predicates in any special way. But a set
are hard-wired into the definitions of truth and satisfaction on a model. In other textbooks, the definitions of truth and satisfaction on a model don’t treat identity predicates in any special way. But a set  only counts as a model if the interpretation function I assigns the set
only counts as a model if the interpretation function I assigns the set 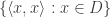 to I. Quine’s model theory differs from the first textbook’s by not having any special truth-or-satisfaction clause for identity statements, and differs from the second’s by allowing models to assign different extensions to
to I. Quine’s model theory differs from the first textbook’s by not having any special truth-or-satisfaction clause for identity statements, and differs from the second’s by allowing models to assign different extensions to  . So on Quine’s model theory,
. So on Quine’s model theory, 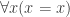 ends up not being a model-theoretic truth either, and the potential counterexamples are all blocked.
ends up not being a model-theoretic truth either, and the potential counterexamples are all blocked.
(For those keeping track: this will, clearly, affect Quine’s overall pro-first-order argument. If he wants to argue that first-order logic is best on the basis of its collapsing model-theoretic, proof-theoretic, and substitutional accounts of logical truth, he’ll have to argue that first-order logic without identity is best — because with identity, first-order logic doesn’t have this property.
Alternatively, as Günther pointed out in the comments to the last post, Quine might instead plump for the modified substitution scheme. Then he can keep identity in, so long as he is willing to argue (as he apparently is) that inclusive (i.e., empty-domain-allowing) first-order logic without names is best. Either way, Quine has to depart from the textbook in some direction or other. As a matter of fact, he departs in all three: he also eschews names and endorses (in Mathematical Logic, anyway) inclusion. So he has a fairly large menu of options here.)
Section 3: The Argument
Here is Quine’s basic argument for EQ-R:
(I). If P is true on all substitution schemes, P is true on all number-theoretic substitution schemes.
(II). If P is true on all number-theoretic substitution schemes, it is true on all models.
(III). If P is true on all models, it is true on all substitution schemes.
(C). Therefore, P is true on all substitution schemes iff P is true on all models.
But (C) is (EQ-R), the desired conclusion. This argument is clearly valid (it’s a standard proof technique to prove a biconditional P iff Q by proving a string of conditionals that start with P, go through Q, and end up back at P again.) But what of the premises?
Some of this, of course, will depend on what “number-theoretic substitution scheme” means. But whatever it means, so long as these are a kind of substitution scheme (and they are!), I is trivial. II and III not so much, though, so we’ll look at Quine’s arguments for them in detail.
3.a: The Argument for III.
Quine argues for this by appeal to
(COMPLETENESS) If  , then
, then 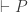
(where 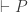 represents the provability of P in any standard first-order system). His reasoning is apparently something like the following. Where S is any (logical-term-preserving) substitution scheme whatsoever:
represents the provability of P in any standard first-order system). His reasoning is apparently something like the following. Where S is any (logical-term-preserving) substitution scheme whatsoever:
- Suppose P is satisfied by every model.
- Then, by COMPLETENESS, it is provable. So there is a proof Pr of P.
- If Pr is the proof of P, then S(Pr) is a proof of S(P).
- Thus, S(P) is provable.
- Therefore, S(P) is true.
The first thing to note is that the move from 4 to 5 relies on the thought that falsehoods can’t be proven or, equivalently, that first-order deductive systems are intuitively sound. ‘Intuitive soundness’ is a notion that crops up in eg Kreisel’s squeezing argument.* The idea here (as Quine puts it, at any rate) is that, among the proof systems we can pick, there are some where we can tell, by inspection, that every individual move takes us from truths to truths. (Or from nothing at all to truths, as happens when e.g. we have an axiomatic system.) Furthermore, we can tell that stringing together series of moves each of which preserves truth will also preserve truth. So we can tell, just by inspection, that there will be no proof of a falsehood. So, since there is a proof of S(P) (line 4), it must be true (line 5).
The second thing to note is that this requires also that, if Pr is a proof, then S(Pr) (the result of taking the proof and replacing each sentence Q in it with S(Q)) is also a proof. This is premise 3. Call proof systems with this property preservational. Notice that not every proof system we might pick is preservational. Suppose, for instance, that we chose a system of semantic tableaux (or “truth-trees”) where only contradictions between literals (atomic predications or their negations) were allowed to close. A proof of ‘ ‘ will be a tree that starts with ‘
‘ will be a tree that starts with ‘ ‘ and ends with ‘
‘ and ends with ‘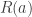 ‘ and ‘
‘ and ‘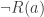 ‘ closing the (only) branch. Now consider the substitution scheme that takes
‘ closing the (only) branch. Now consider the substitution scheme that takes 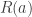 to
to 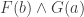 . The tree that you get by taking the above and substituting with this scheme has ‘
. The tree that you get by taking the above and substituting with this scheme has ‘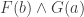 ‘ and
‘ and 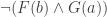 ‘ closing, which is not a proper proof of
‘ closing, which is not a proper proof of 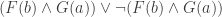 in the imagined system, because it doesn’t have any contradiction between literals.
in the imagined system, because it doesn’t have any contradiction between literals.
This isn’t a huge problem: there are preservational proof systems. And there are intuitively sound proof systems, too. In fact, there seem to be proof systems that are both — standard axiomatized systems seem to have both properties. (They are preservational because whether something counts as a proof is entirely schematic — depends entirely on whether lines of the proof fit certain schemas — and since the substitution schemes preserve logical constants, they can’t make a sentence stop matching a schema when it did before. They certainly seem to be intuitively sound, too, although this is perhaps a more controversial matter.) And good thing, too, because the argument for III goes through only if there are proof systems with both properties. Otherwise, we might have intuitively sound proofs turning into intuitively unsound ones under substitution (violating the move from 4 to 5), or instead intuitively sound proofs turning into things that aren’t even proofs (falsifying 3).
3.b: The Argument for II: Hilbert-Bernays Theorem.
OK, enough of III. It looks secure enough. On to II. Quine’s argument for it relies on a remarkable theorem, a strengthening of the Lowenheim-Skolem theorem, first shown by Hilbert and Bernays:
(HB) If P has a model, it has a constructible model.
A model is constructible iff its domain is a subset of the natural numbers, and each of its predicate extensions is given by a formula of simple arithmetic. That is to say: if F is an n-placed predicate and M a constructible model, then there is some formula A of simple arithmetic, open in n variables, where 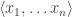 is in F’s extension on M iff
is in F’s extension on M iff 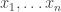 satisfy A. (Note: F is a predicate of the object-language here, but A is an arithmetical formula of the metalanguage.)
satisfy A. (Note: F is a predicate of the object-language here, but A is an arithmetical formula of the metalanguage.)
What does it mean to say that a formula is a ‘formula of simple arithmetic’? We’ll deal with this quite a bit more in Section 4. For now, just note that it will be a formula that uses the primitive vocabulary used in, say, Peano Arithmetic.
The argument for II goes as follows. Call a substitution scheme number-theoretic iff every predicate and term gets replaced for some formula or term of simple arithmetic. We first use (HB) to argue for
(HB*) If Q is true on some model, then for some number-theoretic substitution scheme S, S(Q) is true.
The very basic idea is that, if F is given an extension E on the number-theoretic model, and if A is the formula of simple arithmetic where 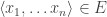 iff
iff 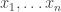 satisfy A, then we can replace F for A. Notice what’s happening here: A appears both in the metalanguage and the object language, so we use the metalanguage characterization of the model (in terms of A) to cook up an object-language substitution scheme (using A). If we do this for all of the predicates and terms in Q, we end up with a sentence S(Q) that basically describes the constructible model we began with, and is true because S(Q) accurately describes that model. In other words: since P is true on the model, and S(Q) says, more or less, that P is true on the model, S(Q) is flat-out true.
satisfy A, then we can replace F for A. Notice what’s happening here: A appears both in the metalanguage and the object language, so we use the metalanguage characterization of the model (in terms of A) to cook up an object-language substitution scheme (using A). If we do this for all of the predicates and terms in Q, we end up with a sentence S(Q) that basically describes the constructible model we began with, and is true because S(Q) accurately describes that model. In other words: since P is true on the model, and S(Q) says, more or less, that P is true on the model, S(Q) is flat-out true.
Since (HB*) is a general principle, it holds even if Q is of the form ~P (for any sentence P). If we substitute in ~P, we get:
(HB~) If ~P is true on some model, then for some number-theoretic substitution scheme S, S(~P) is true.
Now take the contrapositive:
(HBC) If for every number-theoretic substitution scheme S, S(~P) is false, then ~P is false on every model.
But S(~P) = ~S(P), and ~S(P) is false if and only if S(P) is true. Likewise, ~P will be false on a model iff P is true on that model. So (HBC) becomes:
(II) If P is true on every number-theoretic substitution scheme, then P is true on every model.
This is Quine’s second premise. So we have it — if we can substantiate the move from HB to HB*.
4. “Rich Enough for Elementary Number Theory”.
Can we substantiate the move? We can if ‘is a formula of simple arithmetic’ means something like (i) ‘the formula uses Peano Arithmetic’s vocabulary’, (ii) ‘the vocabulary of Peano Arithmetic means arithmetic (‘+’ means plus, and so on), and (iii) Peano Arithmetic is true. In that case, HB ensures that there is a model made out of numbers where every formula’s satisfaction-conditions can be expressed in PA, and for any formula F we can, by uniform substitution, get a formula S(F) that explicitly states those numerical satisfaction-conditions.
4.a: Another Substitution Scheme?
Those are very strong assumptions, though. We might have hoped that we could get away with something considerably weaker. It’s tempting to think that we could have gotten away with mere provability from PA, in which case ‘rich enough for elementary number theory’ would only need to mean something like ‘has the syntactic resources of PA’. The temptation comes, in large part, because we want to think of HB as coding up a kind of logical connection: the premises of mathematics, so to speak, entail that if P has a model, S(P) is true.
Mere syntactic resources won’t be enough, but the tempting thought can be made substitutionally. We might reason like this. Suppose that PA is false (formulated in our ‘vocabulary of number theory’), but has a true substitution instance under a scheme T. HB — the claim which tells us that every satisfiable sentence has a constructible model — tells us that 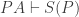 . In this case, since our proof theory is preservational,
. In this case, since our proof theory is preservational, 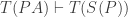 . But since T(PA) is true and our proof theory is intuitively sound, T(S(P)) is true. And T(S(P)) is a substitution instance of P; so the fact that P has a model is enough to show that it has a true substitution instance.
. But since T(PA) is true and our proof theory is intuitively sound, T(S(P)) is true. And T(S(P)) is a substitution instance of P; so the fact that P has a model is enough to show that it has a true substitution instance.
There are two problems with this. The first is that any interesting mathematical consequences of PA will have to involve claims of identity. If Hilbert and Bernays had showed that, when P is satisfiable, 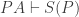 , they surely would have relied on a proof theory that included identity. Since Quine doesn’t reckon identity among the logical constants, it’s not clear whether he can appeal to this claim. Perhaps he could finesse it by adding the axioms of identity theory to PA, but I’d want to see the reasoning spelled out in detail.
, they surely would have relied on a proof theory that included identity. Since Quine doesn’t reckon identity among the logical constants, it’s not clear whether he can appeal to this claim. Perhaps he could finesse it by adding the axioms of identity theory to PA, but I’d want to see the reasoning spelled out in detail.
This first problem may not be a big deal. The second is: there’s no reason at all to think that PA 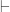 S(P), and at least some inductive reason to think that sometimes it doesn’t.
S(P), and at least some inductive reason to think that sometimes it doesn’t.
First, why is there no reason to think it does? Well, suppose that S(P) is in fact the Godel sentence for PA — the sentence G which says, in effect, that G — it itself — is not provable in PA. Since PA is (various kinds of) consistent, we know that PA 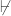 G. But G is going to be true on some constructible model. (It’s true on the standard model of PA, for instance, which is a constructible model.) And there’s just no guarantee that, when we applied S to P, G wasn’t what we ended up with.
G. But G is going to be true on some constructible model. (It’s true on the standard model of PA, for instance, which is a constructible model.) And there’s just no guarantee that, when we applied S to P, G wasn’t what we ended up with.
Of course, this itself doesn’t tell us that there are any P for which S(P) is G; it just raises a spectre of doubt. Here’s another spectre of doubt. The result that Quine appeals to when discussing the Hilbert-Bernays theorem appears to be a corollary of Bernay’s Lemma. Where 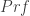 is the formula that captures (via Godel coding — if you’re not familiar, I’ll explain more in the next post) the provability predicate for the “empty theory” (that is, it captures theorem-of-first-order-logic-(without identity(??))-hood) this lemma says that, for any sentence P, there is a substitution scheme
is the formula that captures (via Godel coding — if you’re not familiar, I’ll explain more in the next post) the provability predicate for the “empty theory” (that is, it captures theorem-of-first-order-logic-(without identity(??))-hood) this lemma says that, for any sentence P, there is a substitution scheme  such that
such that
(BL) 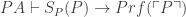
(where 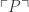 represents P’s Godel number). Since P will be a theorem if and only if
represents P’s Godel number). Since P will be a theorem if and only if 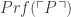 is true, this means that the truth of
is true, this means that the truth of 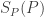 suffices for the theoremhood of P.
suffices for the theoremhood of P.
We can deduce HB* from this as follows:
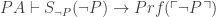 (Bernays lemma, with
(Bernays lemma, with 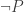 substituted for P.)
substituted for P.)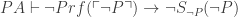 (Contraposing)
(Contraposing) (The internal negation commutes, and the two cancel)
(The internal negation commutes, and the two cancel)
If P is consistent, there is no proof of not-P, and so (assuming PA is true and our proof theory sound) 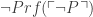 will be true, in which case so will
will be true, in which case so will 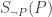 . This means that
. This means that 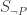 is the substitution scheme we need.
is the substitution scheme we need.
OK, so here’s that next spectre of doubt. The most natural way to show that 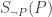 will be provable (as opposed to just true) in PA for every P would be if
will be provable (as opposed to just true) in PA for every P would be if  was provable in PA for every consistent P. This latter sentence says, in effect, that P is first-order consistent. What we might hope to do is to show
was provable in PA for every consistent P. This latter sentence says, in effect, that P is first-order consistent. What we might hope to do is to show
(*) 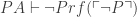
for all consistent P. Then we could use * and line 3 above to conclude (with appropriate subscripts) that PA 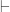 S(P).
S(P).
But, alas, there’s no hope of this. Notice that we already have a procedure for telling whether any sentence Q is a theorem of first-order logic that’s guaranteed to terminate and give us a “yes” answer if Q in fact is a theorem. Moreover, we know that there is no “decision procedure” for determining Q’s theoremhood: there’s no procedure that, for any Q we throw at it, is guaranteed to eventually terminate and tell us “yes” if Q is a theorem and “no” if it’s not.
But if (*) were true for every consistent P, then we would have such a procedure. Just substitute 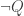 for P. If Q is not a theorem, then there’s no proof of Q, and (since there is a proof of Q iff there is a proof of
for P. If Q is not a theorem, then there’s no proof of Q, and (since there is a proof of Q iff there is a proof of 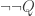 )
) 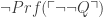 is true. But if the truth of this latter claim guaranteed its derivability from PA (as (*) would have it do), then — since we have a procedure that will always deliver a “yes” verdict when there is a proof — we would have a procedure guaranteed to give us an “yes” verdict whenever we fed it an invalid Q.
is true. But if the truth of this latter claim guaranteed its derivability from PA (as (*) would have it do), then — since we have a procedure that will always deliver a “yes” verdict when there is a proof — we would have a procedure guaranteed to give us an “yes” verdict whenever we fed it an invalid Q.
But we could then stitch these procedures together to cook up a decision procedure for first-order theoremhood. First, spend five minutes on the procedure looking for a proof of Q. Then, if you haven’t gotten an answer yet, spend five minutes looking for a proof of 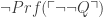 . If you don’t find one in that time, go back to the first, and keep swapping every five minutes. Since no matter whether Q is a theorem or not we are guaranteed that at least one procedure will terminate, this procedure will eventually terminate. If it terminates with a “yes” answer on the “proof of Q” front, then you have the answer “theorem”; if it terminated with a “yes” on the “proof of
. If you don’t find one in that time, go back to the first, and keep swapping every five minutes. Since no matter whether Q is a theorem or not we are guaranteed that at least one procedure will terminate, this procedure will eventually terminate. If it terminates with a “yes” answer on the “proof of Q” front, then you have the answer “theorem”; if it terminated with a “yes” on the “proof of 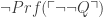 ” front, you have the answer “not a theorem”. But since any such procedure is impossible, (*) must be false after all.
” front, you have the answer “not a theorem”. But since any such procedure is impossible, (*) must be false after all.
Now, none of this shows that PA can’t prove S(P) for every consistent P. It just shows that it can’t (always) do it via (*). But it is difficult to see what other considerations would lead us to think that PA could prove S(P) for every P.
I’d love to know whether PA’s proving power along these lines has been sussed out yet. I have a sneaking suspicion that this is an open problem (in the sense of nobody knowing the answer, rather than in the sense of people actively caring about and working on the answer). But the overall inductive weight of the evidence is pretty hefty against PA’s ability to prove S(P) for every P. I sure wouldn’t place much of a wager on it. And so, at the very least, it leaves the T-using argument above underdeveloped.
4.b: What Can We Say?
Let’s suppose that there are some consistent P for which PA can’t prove the relevant S(P). Then what happens to Quine’s result when PA is true but doesn’t mean arithmetic? Or when PA is false, regardless of whether it means numbers or not?
Suppose first that PA is true, and also means arithmetic. Then we’ll call its standard model  , and following standard usage, let
, and following standard usage, let 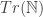 be the set of all of the sentences of L that are true on
be the set of all of the sentences of L that are true on 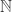 . (Godel’s result shows us, in effect, that no recursive axiomatization can prove every sentence in
. (Godel’s result shows us, in effect, that no recursive axiomatization can prove every sentence in 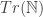 .) Then Quine’s argument at least shows us that, if P is consistent, S(P) is in
.) Then Quine’s argument at least shows us that, if P is consistent, S(P) is in 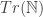 .
.
Now suppose that PA is true but doesn’t mean arithmetic. Then we need to know whether the set of all the truths of our arithmetical language L is again 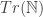 . If PA is true because reality provides the (right sort of) non-standard model, then not all of
. If PA is true because reality provides the (right sort of) non-standard model, then not all of 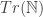 will be true. That’s just the result of PA not proving all of the sentences of
will be true. That’s just the result of PA not proving all of the sentences of 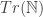 . Suppose Q is a sentence of PA and PA
. Suppose Q is a sentence of PA and PA 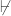 Q; then by the completeness theorem for first-order logic, there will be a model of PA that’s not also a model of Q. And if PA
Q; then by the completeness theorem for first-order logic, there will be a model of PA that’s not also a model of Q. And if PA 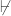 S(P), then (if reality is making PA be true by being the wrong kind of model) it might be that S(P) is false.
S(P), then (if reality is making PA be true by being the wrong kind of model) it might be that S(P) is false.
So, if PA doesn’t mean arithmetic, we can say that Quine’s result holds so long as the set of truths of its language is 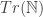 . That might not seem very informative: it comes awfully close to saying something like “Quine’s result holds so long as, for every consistent P, it’s associated S(P) is true”. But we can do at least slightly better if we allow ourselves certain extensions of first-order logic in fixing the language. For instance, Hartry Field notes that if we have a “finitude” quantifier
. That might not seem very informative: it comes awfully close to saying something like “Quine’s result holds so long as, for every consistent P, it’s associated S(P) is true”. But we can do at least slightly better if we allow ourselves certain extensions of first-order logic in fixing the language. For instance, Hartry Field notes that if we have a “finitude” quantifier 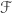 , where
, where 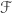 x(Gx) means “finitely many things are G”, then PA plus the axiom
x(Gx) means “finitely many things are G”, then PA plus the axiom
(FIN) 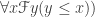
are all true only on “standard” models, i.e., models isomorphic to 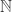 , and therefore PA plus FIN guarantee the truth of
, and therefore PA plus FIN guarantee the truth of 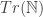 .** Likewise, if the logic of PA is enriched with the omega rule, then we will again have PA
.** Likewise, if the logic of PA is enriched with the omega rule, then we will again have PA 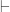 Q for every Q
Q for every Q 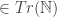 (for our newly omega-enriched
(for our newly omega-enriched 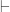 relation), and so the arguments of the Quine post can be re-given.
relation), and so the arguments of the Quine post can be re-given.
But those sorts of enrichments seem especially problematic for Quine. For Quine is trying to argue that substitutional and model-theoretic notions collapse, which in turn relies on the notions applying to the first-order case. If we enrich the logic by introducing new rules or operators, we would have to go back and re-start the argument from the beginning. And it’s entirely unclear how we would do this, since the Hilbert-Bernays theorem it relies on was proven for first-order consistencies, rather than sentences were which “consistent” in the extended sense that would come with an extra inference rule or quantifier. It is not at all clear that if we have an enriched proof relation, and an associated enriched notion of consistency, anything like the Hilbert-Bernays theorem could be proven. If we enrich our proof system in certain ways, the resulting notion of “proof” won’t be effectively decidable, and so there will be no arithmetically definable predicate 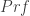 that codes for it, and so there will be no Hilbert-Bernays theorem to appeal to, and so there will be no Quinean collapse argument.
that codes for it, and so there will be no Hilbert-Bernays theorem to appeal to, and so there will be no Quinean collapse argument.
(Perhaps the best Quinean strategy in this area is to go ahead and allow the finitude quantifier, deny it any status as “logic” (including any inferential rules coded into the proof theory), but then insist that we’re only considering interpretations where it means “finitely many”, and so only have to worry about models where it is true of some formula iff finitely many things satisfy the formula. The biggest worry with this approach, I think, would be that the notion of “consistency” would no longer look even reasonably plausible: sentences such as
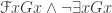
would come out as consistent, when they seem flagrantly not so. If we can make substitutional and model-theoretic accounts of logic collapse only by introducing new resources and then asserting what look like gross implausibilities about what is and is not consistent using those resources, we might legitimately wonder whether the game’s still worth the candle.)
So perhaps we can do no better than saying something like, “Quine’s theorem will apply if PA is true and means arithmetic, or if 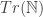 is true (regardless of whether or not it means arithmetic).
is true (regardless of whether or not it means arithmetic).
But what if PA is flat-out false?
Well, suppose PA is flat-out false. (Then 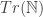 will be flat-out false, too, because it has PA as a part.) But suppose also that there is a substitution scheme U such that U(PA) is true. Then we can ask: is
will be flat-out false, too, because it has PA as a part.) But suppose also that there is a substitution scheme U such that U(PA) is true. Then we can ask: is  true, too? If the answer is yes, then U(S(P)) is also true. (As S(P)
true, too? If the answer is yes, then U(S(P)) is also true. (As S(P) 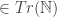 , U(S(P))
, U(S(P)) 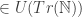 .) And the question as to whether
.) And the question as to whether  is true is (more or less) the question as to whether the chunk of reality that makes U(PA) true is like a standard model of PA, or like a non-standard one. Or, more precisely, it’s asking something like this: if you took each predicate P that appears in PA, looked at the formula F that U swapped P out for, and then built a model M by putting all and only the F-satisfiers in the domain of P, would the result be a standard model of PA? If yes, then
is true is (more or less) the question as to whether the chunk of reality that makes U(PA) true is like a standard model of PA, or like a non-standard one. Or, more precisely, it’s asking something like this: if you took each predicate P that appears in PA, looked at the formula F that U swapped P out for, and then built a model M by putting all and only the F-satisfiers in the domain of P, would the result be a standard model of PA? If yes, then  will be true, and so Quine’s result will follow. Notice that if the answer is “no”, though, that doesn’t quite tell us that Quine’s result does not follow. For there are non-standard models of PA that are also models of
will be true, and so Quine’s result will follow. Notice that if the answer is “no”, though, that doesn’t quite tell us that Quine’s result does not follow. For there are non-standard models of PA that are also models of 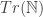 ; perhaps the model built is one of these. If so, then
; perhaps the model built is one of these. If so, then  will again be true and Quine’s result will again follow. But if it’s the wrong sort of non-standard model of PA, S(P) may be false and we can’t rely on collapse.
will again be true and Quine’s result will again follow. But if it’s the wrong sort of non-standard model of PA, S(P) may be false and we can’t rely on collapse.
So that, I submit, is what we can say with confidence: for Quine’s theorem to work, “rich enough for simple arithmetic” needs to mean that there is a substitution scheme U (which might be the identity scheme) for which  is true. A sufficient (but not necessary) condition for this is for the model of PA reverse-engineered from the (true) U(PA) to be a standard model of PA.***
is true. A sufficient (but not necessary) condition for this is for the model of PA reverse-engineered from the (true) U(PA) to be a standard model of PA.***
* Peter Smith argues that there is no genuinely “intuitive” notion of validity (and hence, I imagine, no “intuitive” notion of soundness); to get Kreisel’s argument off the ground, you need rather a semi-technical, quasi-intuitive notion first, and then the argument can show some fully technical apparatus sufficient to capture the semi-technical notion you’ve gotten toward. I think all of that can be accepted while still accepting that any quasi-intuitive notion of soundness you might end up with has this property: no proof that is quasi-intuitively sound has all true premises and a false conclusion. And that’s the strength of premise Quine needs at this stage of the argument.
** If I’m understanding aright, this constraint is strictly stronger than merely making all of 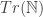 true, as there will be non-standard models of
true, as there will be non-standard models of 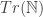 that aren’t also models of PA+FIN.
that aren’t also models of PA+FIN.
*** An equivalent (and less messy-sounding) way to state the condition is that the domain of the so-constructed model (or the extension of “is a natural number” on the model, if the quantification isn’t restricted) is an  -sequence under “<“. But that will hold iff the domain of the quantifiers of L is an
-sequence under “<“. But that will hold iff the domain of the quantifiers of L is an  -sequence under U(<) (or, if the domain isn’t restricted, that the extension of “U(natural number)” is an
-sequence under U(<) (or, if the domain isn’t restricted, that the extension of “U(natural number)” is an  -sequence under U(<)). So a different, not so model-theoretic-sounding way of phrasing the sufficient condition is simply “has as a domain (or as the extension of ‘U(natural number)’) an
-sequence under U(<)). So a different, not so model-theoretic-sounding way of phrasing the sufficient condition is simply “has as a domain (or as the extension of ‘U(natural number)’) an  -sequence under U(<)”.
-sequence under U(<)”.
